|
L'optique géométrique peut être introduite par le principe de Fermat, à partir duquel est déduite la loi de Descartes-Snell. On trouve sur Internet de multiples exemples. Dans ce qui suit, l'aspect original concerne le traitement du miroir sphérique et du dioptre sphérique. Un étude plus complète a été faite dans la rubrique Fermat 4°. À l'époque j'utilisais Cabri Géomètre II, où l'intersection d'un lieu avec un segment n'était pas possible. A. Principe de la construction Le cas étudié est celui d'un dioptre plan. On recherche, pour deux points P et Q donnés de part et d'autre de HK, segment qui sépare deux milieux transparents, homogènes et isotropes, d'indices n et n', la position du point d'incidence I sur le dioptre du rayon qui relie P à Q. Un point M se déplace sur HK. Deux points disposés symétriquement par rapport à M, et séparés de dx, permettent de calculer une valeur approchée de la différence de chemin optique : dx varie de HK/5 à HK/50 afin de pouvoir affiner l'approximation de la position de I. k.dL/n est reporté en ordonnée y sur un axe passant par M et perpendiculaire à HK. Le lieu de y par rapport à M est tracé, et son intersection avec HK donne une valeur approchée de la position du point d'incidence I. B. Résultats Quand on calcule l'écart à la loi de Descartes-Snell, on trouve pour l'exemple choisi les valeurs suivantes :
Sur la Figure d, l'échelle transversale k par laquelle est multipliée l'ordonnée y = dL/n a été augmentée de manière à mieux définir graphiquement l'intersection I du lieu de y avec HK. C. Cas du miroir sphérique On recherche le rayon issu de P qui après réflexion sur le miroir sphérique de centre C passe par Q. P et Q sont des points libres ; M décrit le cercle. m1CM = MCm2 = dq définit l'incrément sur lequel la variation de chemin optique est calculée. k est un facteur d'échelle, variable. La différentielle du chemin optique, corrigée du facteur d'échelle k, est reportée sur le rayon vecteur CM, à partir de M (k.dL = MT). Le lieu de T, lorsque M décrit le cercle, est ainsi une courbe fermée qui coupe le cercle en différents points (4 maximum), solutions du problème. 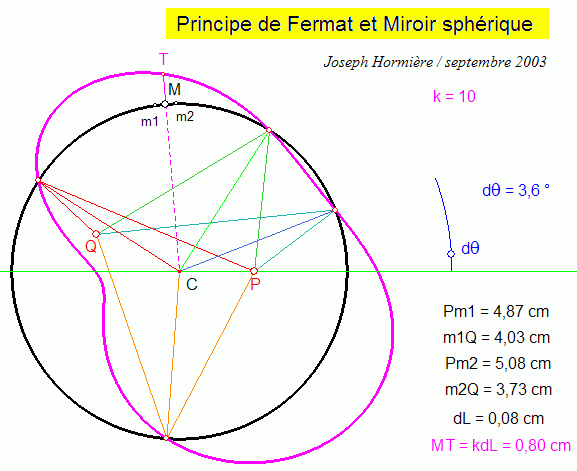 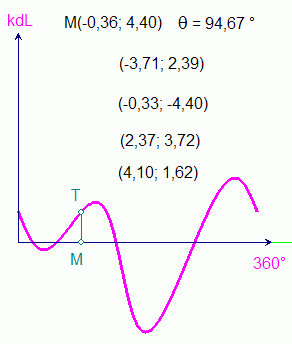 D. Cas du dioptre sphérique La modification de la flèche du dioptre (h) permet de passer du dioptre convexe au dioptre concave avec, comme intermédiaire particulier, le cas du dioptre plan. Les trois réglages complémentaires sont :
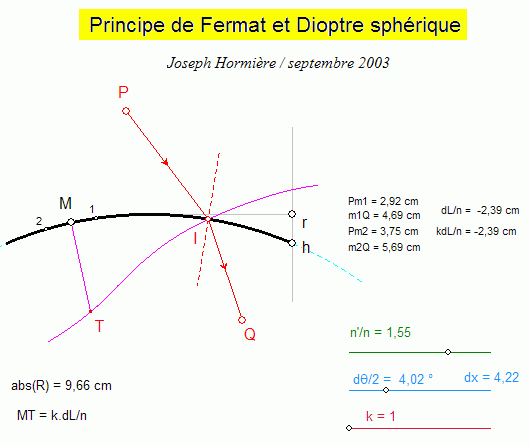 Dioptre convexe 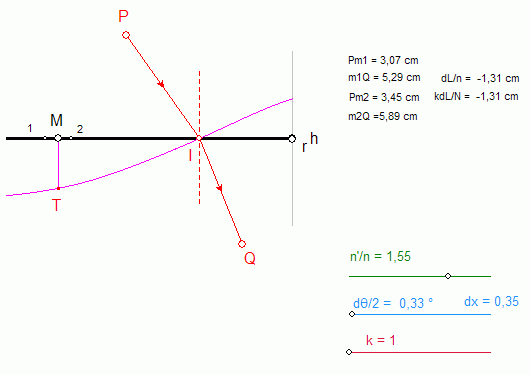 Dioptre plan 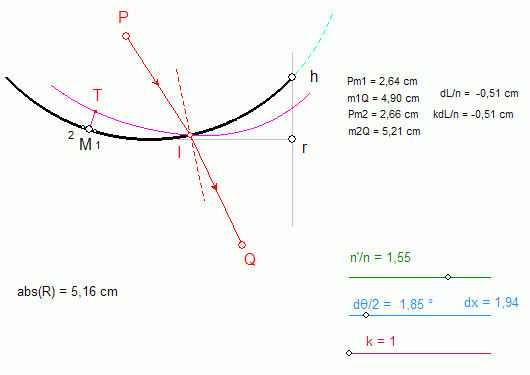 Dioptre concave |
||||||||||
|
|