Le problème est issu de l'étude d'un ophtalmoscope.
Cet appareil permet l'examen du fond d'œil en ophtalmologie. Il fonctionne sur le principe suivant :
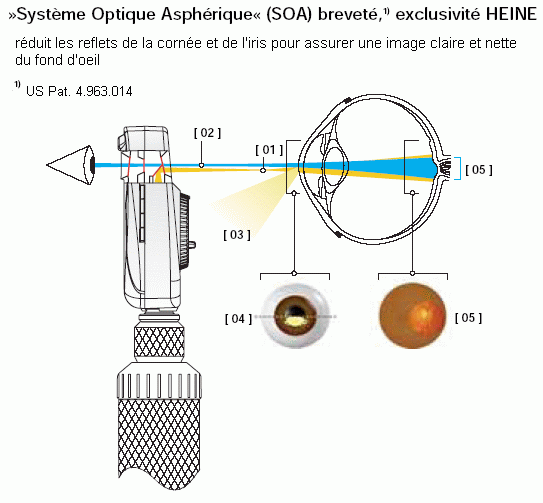
un faisceau lumineux est envoyé à travers la pupille du sujet ; il éclaire le fond de l'œil qui renvoie une faible partie de la lumière reçue ; cette lumière ressort de la pupille du sujet pour entrer dans celle de l'observateur ; quand les deux rétines sont optiquement conjuguées, l'observateur voit la rétine du sujet avec un grossissement de l'ordre de 15.
Pour que l'observateur ne soit pas gêné par le reflet cornéen*, qui risque d'empiéter sur l'image de la rétine qu'il souhaite observer, il faut que les faisceaux d'éclairage et d'observation découpent sur la pupille du sujet des surfaces distinctes. La pupille est ainsi divisée en deux secteurs ou, pour parler de façon plus imagée, séparée en deux portes : une porte d'entrée et une porte de sortie.
Pour une pupille donnée de forme circulaire il semble logique de la découper en deux demi-cercles.
On peut inscrire dans un demi-cercle un cercle, et donc utiliser un faisceau classique de section circulaire. Mais alors le flux entrant dans l'œil, proportionnel à l'aire de ce cercle, ne représente que la moitié de l'aire optimale.
Un faisceau d'éclairage de section elliptique semble être une solution plus avantageuse. Elle est d'ailleurs utilisée par la société Heine (voir, par exemple, le Heine Beta 200 S® Ophtalmoscope).
* la cornée réfléchit une partie de la lumière incidente : petite, certes, par rapport au faisceau d'éclairage, mais grande, par rapport à la quantité de lumière retrodiffusée par la rétine.

L'étude qui suit est donc la recherche de l'ellipse d'aire maximum inscrite dans un demi-cercle.
A. Ellipse de petit axe maximum
Le demi-cercle choisi étant l'inférieur, la première idée qui m'est venue fut de choisir l'ellipse passant par le centre du cercle B et le bord inférieur B'. L'ellipse tangente au cercle, ou le cercle tangent à l'ellipse, m'ont ainsi ramené au problème du cercle surosculateur, déjà abordé dans les approximations d'ellipse par des polycycles.
L'ellipse recherchée a pour axes AA' et BB'. B et B' sont connus. Il reste à trouver A, A' s'obtenant par symétrie.
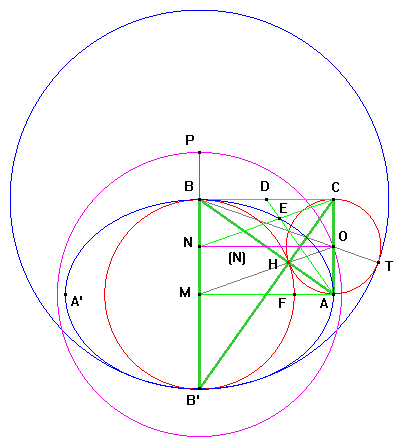
Voilà une façon de construire cette ellipse :
- On prend le milieu M de BB' ;
- puis le milieu N de BM,
- à partir duquel on trace la demi-droite perpendiculaire (N) à BB'.
- On construit le symétrique P de N par rapport à B,
- ce qui permet de tracer le cercle de centre M et de rayon MP
- qui coupe (N) en O.
- On complète le rectangle MNOA : d'où le point recherché A.
- A' est obtenu par symétrie de A par rapport à M.
- Le cinquième point E permettant de tracer l'ellipse avec Cabri est à l'intersection des deux segments NC et AD, où D est le milieu de BC.
Justification de la construction
- L'ellipse recherchée est celle dont le cercle surosculateur en B' est centré en B.
- Or le centre de ce cercle est à l'intersection de la perpendiculaire menée de C à BA avec le petit axe de l'ellipse.
- H, intersection de CB' et BA est centre de l'homothétie de rapport – 1/2 qui transforme le triangle rectangle HBB' dans le triangle rectangle HAC.
- Les cercles de centre M et de rayon MB, de centre O et de rayon OA, exinscrits aux triangles précédents, se correspondent dans la même homothétie ; ils sont en outre tangents en H.
- MO = MH + HO = R/2 + R/4 = 3 R/4 = BO
- Si T est à l'intersection du prolongement de BO avec le petit cercle (O, OA) :
- BT = BO + OT = 3 R/4 + R/4 = R
- Il s'ensuit que le petit cercle est tangent en T au cercle surosculateur.
Remarques
- Le grand rayon de l'ellipse est MA, tel que MA2 = MO2 – OA2 = 9R2/16 – R2/16 = 8R2/16.
MA = a = R√2/2
Le foyer F de l'ellipse, situé entre M et A, est tel que :
e = MF = √(a2 – b2) = √(R2/2 – R2/4) = R/2
- L'aire de l'ellipse est Ae = p MA.MB
Comme MA R√2/2 et MB = R/2, Ae = p R2√2/4.
Comparée à l'aire du cercle de centre M et de rayon MB, Ae/AM = (p R2√2/4)/(p R2/4) = √2.
Comparée à l'aire du demi-cercle dans lequel elle est inscrite, Ae/AB = (p R2√2/4)/(p R2/2)
Ae/AB = 1/√2.
Les trois aires AM, Ae et AB, sont donc entre elles comme les nombres 1, √2 et 2.
Elles sont ainsi en progression géométrique de raison √2.
B. Cas général
La construction a été trouvée par tâtonnements. Je n'ai pas encore cherché de démonstration : avis aux amateurs !
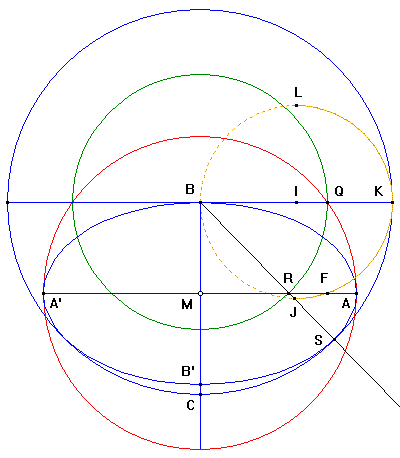
Voilà comment procéder :
- On choisit un point libre M sur un diamètre du cercle d'inscription, tel que BM < BC/2 = R/2.
On cherche le symétrique B' de B par rapport à M.
On trace le demi-cercle JKL, de centre I, milieu du rayon BK.
Ce demi-cercle coupe la perpendiculaire menée de B à BB' en F, foyer de l'ellipse recherchée.
Avec l'outil compas, on reporte la distance BF au point M, de façon à obtenir le point A, sommet du grand axe de l'ellipse.
A' est obtenu par symétrie de A par rapport à M.
Le cercle tracé avec l'outil compas coupe BK en Q.
Le cercle de centre B et de rayon BQ coupe MA en R.
La demi-droite BR coupe le cercle d'inscription en S, point de tangence de l'ellipse.
C. Ellipse d'aire maximum
L'étude de la variation de l'aire de l'ellipse inscrite, lorsque son centre décrit le segment égal au demi-rayon du cercle exinscrit, montre qu'elle passe par un maximum.
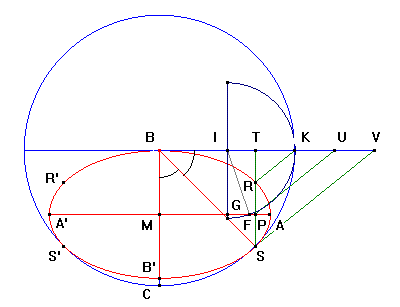
La construction de l'ellipse d'aire maximum a été faite de la façon suivante (tâtonnements toujours) :
- On trace la bissectrice de l'angle CBK qui donne, sur le cercle, le point de tangence S.
- La perpendiculaire menée de S à BK donne le point T,
- duquel on construit le symétrique U par rapport à C,
- puis V, symétrique de K par rapport à U.
- Les parallèles menées de K et U à VS donnent sur ST les points R et P.
- R appartient à l'ellipse recherchée ; on construit son symétrique R' par rapport à CB.
- P appartient au grand axe de l'ellipse ; on mène de lui la perpendiculaire à CB ; l'intersection est le centre M de l'ellipse.
- B' est le symétrique de B par rapport à M.
- Le foyer F de l'ellipse est à l'intersection de cette perpendiculaire avec le demi-cercle défini dans la construction générale.
- CF est reporté sur le grand axe avec l'outil compas, pour construire A et A'.
- L'ellipse est tracée à partir des 5 points choisis parmi : B, R, A, S, B', S', A' et R'.
Remarques
- Le demi petit axe de l'ellipse est les 2/3 de ST.
Or ST = BS cos45 = R√2/2, donc b = BM = TP = R√2/3
Le demi grand axe de l'ellipse est a = MA = BF = √(MF2 + TP2)
MF = MG + GF = BI + √(IF2 - IG2) = R/2 + √((R/2)2 - b2)
MF = R/2 + √((R/2)2 - (R√2/3)2)= R/2 + R/6 = 2R/3
d'où a = √((2R/3)2 + (R√2/3)2 = R√6/3
- L'aire de l'ellipse est alors Amax = p ab = p R√6/3 × R√2/3 = p 2R2√3/9
- Le rapport des aires est : Amax/Ae = (p 2R2√3/9)/(p R2√2/4) = (8Ö3)/(9Ö2)) = 1,089.
Le gain est de l'ordre de 9 %.
D. Conclusions
Pour revenir au problème évoqué au début, un faisceau de section elliptique optimisé permet de gagner sur le faisceau de section circulaire environ 54 % de lumière : ce qui est loin d'être négligeable !
En effet, Amax/AM = (p 2R2√3/9)/(p R2/4)=8√3/9=1,540.
Et pour finir, un petit essai avec l'extension (plugin) Cabri2Plus.
|

